В частности, процесс (2.38), будучи не эргодическим в строгом смысле, эргодичен по отношению к флюктуациям.

Если случайный процесс эргодический, то любая его достаточно длительная реализация представляет свойства всей совокупности. Начальный момент k-ro порядка для такого процесса и его корреляционная функция удовлетворяют условиям:

R(0] = m,Rk(r)] = <r(r)>; (2.39)

*t (X) = lilt К (О Ъ (t + X)] = & {t) $r (t + Х)>

для любой г-й реализации процесса.

Эргодичность процесса создает большие удобства для опытного определения статистических характеристик, так как позволяет получить их из одной достаточно длительной реализации случайного процесса.

2.6. Многомерный нормальный закон распределения. Нормальные случайные процессы

Рассмотрим многомерный нормальный закон распределения, имеющий вид [1,16]:

w (xh х2.....хп) =

aia2... а„л/(2я)л£>

(2.40)

1 = 1 * = 1

где

1 р12 ... р/п р2/ 1 . . . Р2п

Pnl Рп2

- определитель*; Aik - алгебраическое дополнение элемента pik определителя; pik = Pki - некоторые числовые величины, удовлетворяющие условию р,* < 1 при / Ф к. В частности, при п = 2, обозначая pi2=P2i=p, получаем Z>=l-p2, Ai2=A2i=p, Лц=Л22=1 и двумерный нормальный закон распределения случайных величин £ь £2 принимает вид:

*] Краткие сведения об определителях см. в приложении.

и>2 (хи х2) =

oio227rVl -р1

2(1-р2)

(xi-ад2

-2р

(х\-а{)(х2-а2) (x2-a2j

- + -2-

olg2 О 2

(2.41)

Для того, чтобы раскрыть смысл величин аи а2, о\9 о2 входящих в (2.41), достаточно определить одномерные законы распределения случайных величин £j и £2:

т (х\) = J w2 (хи х2) dx2 ,

wi (х2) = J w2 (хи х2) dxx.

Для функции w2 (хи х2) вида (2.41) интегралы в правых частях этих ажений сводятся к табличным и одномерные законы распределения водятся к виду Г11:

wi (хг) =

wi (х2) =

<2ж>

ехр

(х\-ахУ

2Л

V2rca2

ехр

(х2-а2) 2<?2

Црим образом, одномерные законы распределения случайных величин £1 Ъ%2 получаются нормальными вида (2.19), а величины о2ь а\ и а\а2 дставляют их дисперсии и средние значения.

Для определения величины р, входящей в (2.41), нужно найти кова-рйацию случайных величин и

М2(ЪиЪд= J J (xi-ax)(x2-a2) w2 (хи х2) dxxdx2 .

Для функции w2 (хи х2) вида (2.41) этот двойной интеграл сводится к 1юизведению табличных однократных интегралов и выражение для кова-ррации случайных величин £1 и приводится к виду [1]:

af2($b§2) = poia2,

Шкуда

Р = М2Й1,&.Уо№. (2.42)

Таким образом, величина р представляет коэффициент корреляции мевду случайными величинами, определяемыми нормальным двумерным законом распределения (2.41).

Аналогично можно показать, что и в n-мерном нормальном законе распределения (2.40) величины о2ь о22, о2 представляют дисперсии аи а2у ...,ял - средние значения, р - коэффициенты корреляции случайных величин £ь 2. определяемых законом распределения. В частном случае, когда случайные величины не коррелированы и р,у = 0, i Ф у, нормальный многомерный закон распределения принимает вид

wn (хи х2у хп) = II -т=- ехр 0/\2зс

(*/-fl/)2

(2.43)

т.е. представляет произведение одномерных нормальных законов распределения.

Таким образом, если случайные величины подчиняются многомерному нормальному распределению, то их некоррелированность является достаточным условием их независимости. Для произвольного закона распределения это несправедливо.

Как уже отмечалось, реализации случайного процесса с требуемой точностью могут определяться дискретными выборками отсчетов, а сам случайный процесс может определяться многомерным законом распределения случайных величин, составляющих выборку. Случайный процесс £ if) называется нормальным (гауссовым), если законы распределения любого л-го порядка для совокупности случайных величин £ (f*), к-\, 2, л, нормальные, т.е. определяются формулой (2.40). Поскольку величины аи о/ и ру, входящие в формулу (2.40), для любой выборки дискретных отсчетов представляют значения функций о$ ( ) и В$ fa, tj) в соответствующих временных сечениях, то нормальный случайный процесс полностью определяется этими двумя характеристиками. Поэтому для нормальных процессов условия стационарности в широком смысле достаточны и для определения строгой стационарности и корреляционная теория имеет неограниченную область применения. Для нормального стационарного процесса

а (0 = а$ = const; 1% (tu t2) = В$ (т); а\ = В$0 (0) = В^ (0) - а\ = const; р*(т)= 0(t)/gV

и при использовании выборки отсчетов с интервалом дискретности At=T/n n-мерный закон распределения, определяющий этот процесс, имеет вид:

1=1 7=1 *

где входящие в определитель D величины равны

2.7. Спектральное представление стационарных случайных процессов

В качестве спектральной характеристики стационарного случайного процесса будем использовать осредненное по множеству реализаций значение спектральной плотности мощности.

Рассмотрим одну из реализаций xk (t) стационарного случайного процесса £ (Г). Заменим ее усеченной реализацией x&(t\ равной нулю вне интервала г|Г/2. В соответствии с (1.10), (1.11) усеченная реализация xa(t) может быть разложена в ряд Фурье с интервалом между гармониками ДМ/Г и комплексной амплитудой гармоники/

Cu<fi>=\ J x*r(t)e Ut. (2.46)

* -772

Средняя мощность, приходящаяся на единицу полосы спектра реализации xkT(t\ при этом равна

GkT(f)= tftf(/)P = 7UrO)Ur(-/) =

т/2 т/2

-т/2 -772

Г/2 Г/2

= \г\ \хкТ(г,)хкТfe) с** <ft, db . (2-47)

-Г/2 -Г/2

Осредним GkT (J) по множеству реализаций, положив процесс стационарным (операцию осреднения обозначим чертой сверху):

772 772

Gf) = -±г j j В%Т(t\ -t2) e(,rt) dt\ dt2 .

-Til -772

Введя вместо f i новую переменную x = fi- f2, получим

Г *2- (t)

G(f)= 1- J % (т) er J Л2 A. (2.48)

В этом выражении внешний интеграл (по х) имеет пределы интегрирования от -Г до Г, так как

*min = *imin - fema* = - Г/2 - Г/2 = - Г, хщах = * imax ~ fcmin = Г/2 + Г/2 = Г.

Функция By - f2) = %т (h) £,т (h) отлична от нуля лишь при условии, что оба значения аргумента t принадлежат области [-Г/2, Г/2] ненулевых значений функции £г(0- Поэтому пределы интегрирования для внутреннего интеграла определяются как крайние значения переменной интегрирования t2 при фиксированном х, удовлетворяющие этому условию, а именно:

для х > 0, т.е. при t\ > t2,

2тш(х) = Г„ип = -Г/2; Г2 шх(т) = тах-М = Г/2-х|;

для х < 0, т.е. при t\ < t2,

*2тю (X) = fmin + М = Г/2 + /2шах (т) = W = Г/2 .

В обоих случаях для разности fomax (х) - fcmm (х)] получается одинаковое значение

[Umax (X) - *2min (х)] = Г- т| .

Поэтому (2.48) принимает вид

ОгЖ= %(х) (\ - Щ е**А .

Переходя к пределу при Т- < , получаем

G$ = limGr~(/)= f (х)е^тЛ =

Г-х i

= J fi (х) cos 2тг/х dx - j j J% (x) sin 2тс/х dx. (2.49)

Кроме того, по-прежнему предполагается, что процесс является действительной функцией времени.

&<0 = 2Gfe</).

(2.52)

В силу четности В$ (/) второй интеграл равен нулю и

G$(/) = J В$ (т) cos 2%ft dx = 2 JJ?$ (т) cos 2я/х dx, (2.50) т.е. G$ (/) - также четная функция.

Функцию частоты <%(/), представляющую осредненную по множеству реализаций спектральную плотность мощности стационарного процесса, называют энергетическим спектром. Это название, укоренившееся в литературе по радиотехнике, которым будем пользоваться и мы, нельзя признать удачным, ибо оно не соответствует фактической размерности величины (*£ (/) Бели равенство Парсеваля (1.18), полученное для детерминированных сигналов с конечной энергией, действительно содержит энергетический спектр, т.е. спектральную плотность энергии сигнала, то для стационарных случайных сигналов мы принципиально не можем воспользоваться аналогичной характеристикой. Стационарный случайный сигнал, строго говоря, имеет неограниченную длительность (иначе нарушались бы условия стационарности). Поэтому при конечной средней мощности он обладает бесконечной средней энергией, а в случае ограниченной ширины спектра - и бесконечной спектральной плотностью энергии. Поэтому для характеристики стационарных случайных сигналов используется спектральная плотность мощности. Заметим, что сигналы с ограниченной энергией, для которых получено равенство Парсеваля (1.18), можно характеризовать только спектральной плотностью энергии, ибо спектральная плотность мощности для них обращается в нуль. Неудачный термин энергетический спектр в данном случае привился, по-видимому, . потому что размерность спектральной плотности мощности совпадает с размерностью энергии (но не спектральной плотности энергии!):

Gr(f) = &/Af=PT.

Из (2.50) следует, что энергетический спектр G$ (J) и корреляционная функция В$ (х) стационарного случайного процесса (t) связаны преобразованиями Фурье, и поэтому можно записать обратное преобразование:

Bt (J) = (/)cos 2фdf = J2G$(f) cos 2nftdf. (2.51)

Таким образом, энергетический спектр стационарного случайного процесса однозначно определяет его корреляционную функцию, а если этот процесс нормальный с известным средним значением, то он определяет и все его статистические свойства. Полученный результат, показывающий, что корреляционная функция и энергетический спектр стационарного случайного сигнала связаны между собой так же, как детерминированный сигнал и его спектр, носит название теоремы Хинчина-Винера,

Величина G (/), определяемая по формуле (2.50), дает спектральную плотность средней мощности, отвечающую случаю использования двустороннего комплексного спектра. Для одностороннего спектра, отвечающего гармоническим базисным функциям, спектральная плотность

При т = 0 из (2.51) получаем очевидное соотношение, связывающее среднюю мощность и ее спектральную плотность:

*б(0)= jGfc(04f= Jft<04f. (2.53)

- о

Величину площади под кривой одностороннего энергетического спектра, отнесенную к спектральной плотности на некоторой характерной частоте /о (обычно соответствующей максимуму спектральной плотности), называют шириной полосы энергетического спектра:

ДГ= f <§t(f)df. (2.54)

Она равна основанию прямоугольника, имеющегд высоту (/ь), равновеликого по площади средней мощности сигнала В$ (0) (рис. 2.4). На основании (2.50) спектральную плотность средней мощности при /=0 можем записать в виде:

& (0) = 2<% (0) = 2 (т) dx. (2.55)

Если случайный процесс эргодический, то осреднение по множеству реализаций можно заменить осреднением по времени:

Г/2 в*

*t (0) = lim J К* (О]2 Л = J Gfe (0 4f <2-56)

&(fo)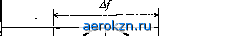

0 fo f

Рис. 2.4

Преобразования Фурье (2.50), (2.51) применимы только для стационарных процессов с нулевым средним значением, так как в противном случае В$ (т) - а\ при т -> и не выполняется условие абсолютной интегрируемости функции В$ (т):

J Я$(т)Ж*АГ, (2.57)

необходимое для применения преобразования Фурье.

Корреляционная функция В^(х) и энергетический спектр G(f), как всякая пара функций, связанных преобразованием Фурье, подчиняются следующей закономерности: чем шире спектр, тем уже корреляционная функция (меньше время корреляции), и наоборот.

2.8. Случайный процесс типа белого шума

Рассмотрим центрированный стационарный случайный процесс с равномерным энергетическим спектром в ограниченной полосе:

G(/)= (W2 при|/К* (2.58)

В соответствии с (2.51) корреляционная функция такого случайного процесса имеет

/ ч No f <*-л. jr No sin 2я£т /Л пч

(х)=-у )cos2*fzdf= --- . (2.59)

Дисперсия (средняя мощность) этого процесса

о2* = В$(0) = (2.60)

При фиксированной спектральной плотности No дисперсия (2.60) неограниченно увеличивается с расширением спектра. Нормированная корреляционная функция процесса, задаваемого энергетическим спектром (2.58), равна

Р5 (г) = В$ (х)/а\ = sin 2я£х/2я£т. (2.61)

Согласно теореме Котельникова реализации случайного процесса с ограниченным спектром полностью определяются выборкой случайных величин, представляющих его дискретные отсчеты через интервалы At - \12&. Как следует из (2.61), при т = kAt = kJ& Pt 00 = 0, т.е. отсчеты через равномерные интервалы А/, принадлежащие выборке, полностью определяющей стационарный случайный процесс с равномерным энергетическим спектром, будут некоррелированы. Если стационарный процесс, обладающий энергетическим спектром вида (2.58), является к тому же нормальным, то из некоррелированности отсчетов, составляющих выборку, следует их независимость (см. § 2.6). Такой процесс полностью определяется одномерным нормальным законом распределения его значений в произвольном временном сечении.

Эти свойства сохраняются при любой ширине равномерного энергетического спектра случайного процесса. В пределе прн °о и At - 0 случайный процесс с равномерным энергетическим спектром характеризуется отсутствием корреляции между сколь угодно близкими его отсчетами. Такой случайный процесс носит название белого шума. Корреляционная функция белого шума удовлетворяет условию:

при т = 0, при т Ф О,

а его дисперсия (средняя мощность) а\ = В$ (0) -°°.

Корреляционная функция белого шума математически может быть определена с помощью 5-функции, обладающей следующими свойствами:

8(х)= (Г приТ = ° (2.62)

[0 при т * 0;

8(т)Л=1. (2.63)

Простейшей моделью 5-функции может служить функция получающаяся в результате предельного сжатия прямоугольного импульса единичной площади шириной а с амплитудой 1/а, симметричного относительно оси ординат (рис. 2.5). Если семейство этих импульсов представить однопараметрической функцией вида Л(х, а), то можно записать, что

8(т) = НтД(т,а). (2.64)

aj>a2>a3>.. .xXn->0

Рис 2.5

Можно назвать целый ряд других семейств однопараметрических функций, удовлетворяющих условию (2.64). В частности, однопараметрическое семейство одномерных нормальных законов распределения вида

w Ос, о) =

ехр

удовлетворяет условию (2.64):

lim w (х, о) = 8 (х).

Таким образом, 8-функция представляет собой обобщенную функцию, получающуюся предельным переходом вида (2.64) от семейств однопараметрических функций Д(т, а) различной формы, обладающих общим свойством сжатия при а->0 в бесконечно узкий пик единичной площади.

В случае, когда 8-функция стоит под знаком определенного интеграла в качестве сомножителя, она обладает своеобразным фильтрующим свойством: в результате интегриро-

вания выделяется значение стоящей при ней в качестве сомножителя функции, отвечающее величине переменной интегрирования, обращающей в нуль аргумент 5-функции. Действительно, если функция /Ос) непрерывна в бесконечно малой е-окрестности точки х\, то учитывая, что 8 Ос - jci) = 0 при х - jci > е, получаем

J f{x) 8 (х - *,) ах = j f(x) b(x-xx)dx =

-~ xi-e

Jti+€

=/C*i) J 8(x-jc,)dx=/0ci). (2.65)

jtr-e

Используя 8-функцию, корреляционную функцию белого шума можно представить в

В*(т)=8(т). (2.66)

Легко убедиться,что корреляционной функции вида (2.66) соответствует равномерный энергетический спектр со спектральной плотностью G (/) = NqI2 на всем интервале частот от - к до -н . Используя (2.50) и учитывая фильтрующее свойство 5-функции получаем

G(/)= /я<(т)е**А = -f J8(x)e-A=.

Белый шум, определяемый как случайный процесс, отвечающий бесконечно широкому равномерному энергетическому спектру, представляет абстракцию, физически не реализуемую. Его нельзя задать математически как случайный процесс: нельзя задать одномерный закон распределения, определяющий нормальный белый шум, поскольку дисперсия его бесконечна. Мы можем лишь характеризовать локальные свойства белого шума в частотном и временном измерениях пространства сигнала: однородность спектральной плотности мощности и некоррелированность сколь угодно близких по времени отсчетов. Однако эта абстракция оправдана тем, что специфические свойства белого шума переносятся и на случайные процессы с ограниченной мощностью (дисперсией), отвечающие ограниченному участку равномерного спектра, выделяемому входным устройством. Хотя при этом время корреляции шума уже конечное, отсчеты многомерной выборки, следующие через интервал At=l/2& и полностью задающие шум при ограниченной ширине его спектра, как было показано, будут некоррелированными. Таким образом, корреляционные свойства белого шума полностью переносятся на дискретную выборку, определяющую стационарный процесс, обладающий равномерным спектром в полосе, ограничиваемой входным устройством реальных систем. Корреляционная функция и форма энергетического спектра шума на выходе системы, при действии на его входе белого шума, полностью определяются параметрами системы с точностью до масштабного коэффициента No характеризующего уровень входного шума. Это, кстати, делает белый шум весьма удобным эталонным сигналом при определении характеристик линейной системы (импульсной переходной функции, передаточной функции, ширины полосы пропускания).

Для того чтобы шум, действующий на входе системы, мог рассматриваться как белый , достаточно, чтобы он имел относительно равномерный энергетический спектр в пределах полосы пропускания входного устройства системы; характер энергетического спектра

шума вне этой полосы не имеет значения. Таким образом, благодаря ограниченной полосе пропускания реальных систем белый шум обретает физическую реальность.

2.9. Узкополосные случайные сигналы

Стационарный случайный сигнал называется узкополосным, если его односторонний энергетический спектр if) сосредоточен в окрестности некоторой частоты /о в относительно узкой полосе: Af <*/о (рис. 2.6).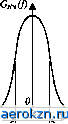

Ряс 2.6

Выразим корреляционную функцию такого случайного сигнала через его односторонний энергетический спектр (/):

Перейдем от абсолютного значения частоты/к расстройке/=/-/о Тогда получим

Д$(т)= ]Gm(f)cos [2K(f0+f)z]dfy (2.67)

где Gmif) -*§(/о +f) - низкочастотный узкополосный энергетический спектр, соответствующий переносу начала отсчета частоты в точку/о (рнс. 2.6). Так как расстройка/ в области А/* ненулевых значений энергетического спектра меняет знак, то при переносе начала отсчета в точку /о односторонний энергетический спектр трансформируется в двусторонний спектр Gm(f), сосредоточенный в области \f\Hf/2<fo. Поскольку для значений f<-/о, лежащих далеко за границами области ненулевых значений спектра, можно принять Gm(f) = 0, то нижний предел интегрирования в (2.67) можно расширить до -©о и записать

Л*(т)=[7

Gm(f) cos (2nfz)df

cos 2л/от -

jGH,(r)sin(2<t)<

sin 2я/от.

(2.68)

Если энергетический спектр симметричен относительно нового начала отсчета частоты, то Gm(f) - четная функция/и интеграл во втором слагаемом правой части (2.68) обращается в нуль. В этом случае получаем

где Bm (т) - корреляционная функция огибающей, определяемая низкочастотным энергетическим спектром Gnif) -

Таким образом, корреляционная функция узкополосного сигнала, энергетический спектр которого симметричен относительно частоты/о может быть представлена в виде ам-плитудно-модулированного колебания с частотой /о, огибающая которого представляет корреляционную функцию огибающей рассматриваемого узкополосного сигнала.

(т) = £jG ,(f) cos (2я/Ч) dfj cos 2*fyz =

= BH4(x)cos27c/p0t, (2.69)

Глава 3

СТАТИСТИЧЕСКАЯ ТЕОРИЯ ОБНАРУЖЕНИЯ СИГНАЛОВ

3.1. Классификация задач обнаружения сигналов

Сформулируем задачу обнаружения сигналов. Пусть имеется некоторое число различных сигналов щ (/), лишь один из которых может передаваться на интервале наблюдения. Сигналы могут быть либо детерминированными, либо квазидетерминированными, либо случайными с заданными вероятностными характеристиками. На вход приемного устройства поступает реализация случайного сигнала, представляющего смесь переданного полезного сигнала щ (i) и случайной помехи п (г)

у (г) = и, (0 + л (г). (ЗЛ)

При этом одна и та же реализация суммарного сигнала у (t) может получиться для различных вариантов переданного сигнала в сочетании с некоторой реализацией случайной помехи

л (г) = у (0- *(*). (3.2)

Таким образом, после приема сигнала у (t) могут быть выдвинуты разные гипотезы о том, какой из сигналов щ (i) был предан. Задача статистической теории обнаружения сигналов - дать метод выбора наиболее достоверной из этих гипотез.

В зависимости от числа возможных вариантов передаваемых сигналов задачи обнаружения можно подразделить на бинарные и много-альтернативные.

В бинарных задачах на интервале наблюдения может передаваться один из двух сигналов. Частным случаем бинарной задачи является обнаружение факта передачи или отсутствия единственного сигнала, так как отсутствие сигнала на интервале наблюдения эквивалентно нулевому сигналу. К числу бинарных задач обнаружения относятся задачи обнаружения радиолокационного сигнала, распознавания символов двоичного кода и др.

В многоальтернативных задачах требуется идентифицировать принятый сигнал с одним из п сигналов с известными характеристиками, где

п > 2. К числу таких задач относится распознавание символов кода с основанием более двух,прием функциональных команд, переданных по командной радиолинии и др.

По характеру полезных сигналов можно выделить следующие классы задач обнаружения:

1) обнаружение сигналов с известными параметрами на фоне шума (цифровые системы связи при наличии синхронизации, командные радиолинии др.);

2) обнаружение сигналов с неизвестными параметрами на фоне шума (радиолокационное обнаружение, цифровые системы связи без канала синхронизации)

3) обнаружение случайных сигналов на фоне шума (сейсмические системы обнаружения, радиоастрономия, радиоразведка).

3.2. Общая постановка бинарной задачи обнаружения. Критерий Байеса.

Результат наблюдения на интервале Т реализации у (/), представляющей смесь полезного сигнала и шума, можно характеризовать выборкой из N значений (уи Уг, Улг), т.е. представить в виде вектора у в N-мерном пространстве. Обозначим через Я0 и Н\ гипотезы, соответствующие двум возможным вариантам передаваемого сигнала щ и щ (в случае обнаружения единственного сигнала Я0 - гипотеза о его отсутствии, а Я] - гипотеза о его наличии). В бинарной задаче верна либо гипотеза Я0, либо гипотеза Н\. Поэтому при решении задачи обнаружения возможен один из четырех исходов:

1) выбрана гипотеза Я0 и верна гипотеза Я0;

2) выбрана гипотеза Яь а верна Яо;

3) выбрана гипотеза Н\ и верна Яь

4) выбрана гипотеза Яо, а верна Н\.

Первый и третий исходы соответствуют правильным выборам, второй и четвертый - неверным.

Пусть известны априорные вероятности Ро и Pi передачи сигналов щ и Hi. Припишем каждому из четырех возможных исходов решения задачи обнаружения некоторую стоимость, характеризующую те потери (или выигрыш), которые будут при этом исходе. Обозначим эти стоимости соответственно Соо, Сю, Сц и Coi (первый индекс обозначает выбранную гипотезу, а второй - правильную). Будем строить наше правило решения таким образом, чтобы средние потери были минимальными (критерий Байеса). Величину средних потерь назовем средним риском и обозначим

буквой R. Обозначим условные вероятности перечисленных исходов: Р (Я0Я0), Р (#i#o), Р (#i#0, и Р (#о|#0, где первой стоит выбранная гипотеза, а второй - правильная. Тогда средний риск

R = СооРоР (#о|#о) + С10РоР (#,!#<,) + СпРхР(ЩНх) + СогРхР (tf0#i), (3.3)

Примем, что стоимости потерь при ошибочном решении Сш> 0 и С0\ > О, тогда как при правильном решении мы имеем выигрыш или отрицательные потери: СЬо^О и СцО. Таким образом, всегда будут выпол-

о; Coi>Cu. (3.4)

Правило решения сводится к разбиению пространства Z наблюдения N-мерного вектора у на две части Zo и Zb соответствующие принятию гипотез Но и#1 (рис. 3.1).

Оптимизация правила решения сводится к такому выбору границ разбиения, определяющих решение, который минимизирует средний риск R.

Поскольку для области Zo принимается гипотеза Я0, а для области Z\ - гипотеза Ни то

где p (у\щ) и p (у\щ) - плотности условных вероятностей появления реализации у (t) при условии, что соответственно были переданы сигналы щ и щ. Интегралы от этих плотностей вероятности по областям Zb и Z\ пространства реализаций у (t) дают вероятность того, что при этом реализация будет принадлежать данным областям и соответственно будут приняты гипотезы Но и Н\.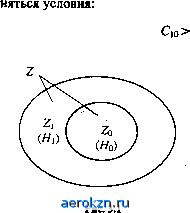

Подставляя в (3.3) выражения (3.5)-(3.8), получаем

Я = СооР0 f р(уЫ<*У + СюРо jp(y\uo)dy +

Zo Z,

+ CnP, J р (у|щ) dy + CoiPi J p (у\щ) dy . (3.9)

Z, Zo

Учитывая, что

J Р (y\ud dy =1 - J p (y\ud dy, (3.10)

Z, Zo

получаем

R = PoCio + PiCu + J [Pi (Coi - Си) p (y\ux) -

-Ро(Сю-СЬо)р(уМУ- (З.П)

Первые два члена в (3.11) соответствуют фиксированным потерям, не зависящим от выбора границ области Zo. Поэтому для минимизации R нужно выбрать область Zo так, чтобы она включала все отрицательные (и только отрицательные) значения подынтегрального выражения в (3.11), т.е. из условия

Pi (Coi - Си) р (уЫ - Ро (Сю - Coo) Р (у\щ) < 0 (3.12)

Учитывая условие (3.4), неравенство (3.12) можно переписать в виде

. Pq(Cio-Cqo) п п.

Pi(C0l-(Cn)

а правило решения в виде

р(уи\) £ Ро(Сю-Соо) .

ТШ) t Pi (Coi ~(Си) w }

Такая запись означает, что при знаке > принимается решение Ни а при знаке < - решение Нъ

Левую часть неравенства (3.14) называют отношением правдоподобия и обозначают

Смысл термина очевиден: более правдоподобна та из гипотез, которой соответствует большая плотность вероятности получения данной реализации у (г). Каждой реализации случайной функции у (t) при любой размерности, используемой для задания дискретной выборки, соответствует

определенная величина отношения плотностей вероятностей в правой части (3.15). Поэтому отношение правдоподобия Л (у) является одномерной случайной величиной.

Как будет видно из дальнейшего, отношение правдоподобия является фундаментальным соотношением, используемым не только в статистической теории обнаружения сигналов, но и в теории оценки параметров сигналов.

Правая часть (3.14) представляет фиксированную величину, зависящую только от априорного распределения вероятностей передачи сигналов и от выбора стоимостей верных и неверных решений. Она определяет порог решающей схемы

П = Л) (С10 - Соо) / Рг (Сох - Сп). (3.16)

Таким образом, критерий Байеса сводится к критерию отношения правдоподобия

Л (у) 8ц. (3.17)

Важно отметить, что распределение априорных вероятностей и стоимостей влияет лишь на выбор численного значения порога, но не влияет на процедуру обработки данных, заключающуюся в вычислении А (у). Поэтому уточнение стоимостей и априорных вероятностей, которые часто носят характер не очень строгих экспертных оценок на основе интуиции или предшествующего опыта, не влияет на решающую схему, а требует лишь перестройки уровня порога.

Так как обе части неравенства (3.17) положительны, то вместо отношения правдоподобия Л (у) можно использовать в неравенстве его логарифм, являющийся монотонной функцией, и записать критерий отношения правдоподобия в форме

In Л (у) 8lnr, (3.18)

которая очень удобна, так как во многих случаях плотности вероятности р (у\ид являются показательными функциями.

Найдем выражение для Л (у) в случае детерминированных сигналов щ(г) и помехи п (г), представляющей нормальный белый шум. Пусть спектр шума ограничен в пределах полосы Д£ В этом случае реализации шума п (t) в соответствии с теоремой Котельникова могут быть заданы дискретной выборкой (п\,П2, ...,лт) с интервалом между отсчетами At = \l2Af. Поскольку все эти отсчеты будут независимыми случайными величинами (см. § 2.8), многомерный нормальный закон распределения,

определяющий плотность вероятности и>ш(льЛ2 пт)9 может быть представлен в виде (2.43) при а, = аш*.

w. (пи т,пт) = \jnn П ехР =

(2зиГ,

-7-14 (ЗЛ9)

где пк - отсчеты белого шума п (f), следующие через интервалы At = 1/2Д/, m - общее число отсчетов на интервале Т действия сигнала (т = Г/Аг = 2ГАД

Плотность вероятности р (у\ид появления реализации входного сигнала у (t) = щ (i) + п (t) соответствует плотности вероятности wm [у (0 ~Щ (*)] реализации шума n(t)=y (t) - щ (*). Дискретные отсчеты этой реализации шума nk-y (tk) - Uj (tk) - Ду,*, а соответствующая m-мерная плотность вероятности

Р (у\щ) = и>ш (Аул, Дуд,..., Ayim) =

Тогда

А(у)= Г^Лй =еХр{- -V t [АЛ-А/4 = и>ш(у-ио) г [ 2а ш ~ J

= ехР ( 0 I, {Ь (*) ~ их (h)f - \У Ш - ио (h)]2} Д/j . (3.21)

где No = а2щ/Д/- спектральная плотность шума.

С учетом (3.21) критерий (3.18) для принятия решения о выборе гипотезы по известной реализации входного сигнала у (г) принимает вид

In А(у) = - jr X {Ь (fc) - Щ (h)f -

-[ya*)- o(**)]2}Af (3-22)

При достаточно большой ширине полосы Д/и соответственно малом At сумму можно заменить интегралом и записать критерий (3.22) в виде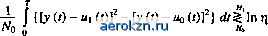

(3.23)

Сопоставляя левые части (3.23) и (1.20), легко видеть, что в случае обнаружения сигнала на фоне белого шума критерий Байеса сводится к сравнению расстояний в пространстве сигналов между принятой реализацией у (г) и передаваемыми сигналами щ (г) и щ (/).

При использовании общего байесовского подхода к задаче обнаружения сигналов большую практическую трудность представляет выбор стоимостей Су, определяющих порог т|. Поэтому при решении ряда практических задач используются критерии, представляющие модификации или частные формы критерия Байеса, позволяющие обойти эту трудность.

В последующих параграфах мы рассмотрим их применительно к конкретным задачам обнаружения сигналов.

3.3. Синхронный прием символов двоичного цифрового кода при действии белого шума. Критерий идеального наблюдателя

Пусть двоичный цифровой код используется для передачи значения некоторой случайной величины. Тогда ошибочные решения при приеме символа k~ro разряда кода могут заключаться либо в приеме 1, когда был предан 0, либо в приеме 0, когда была передана 1. Абсолютное значение вызываемой этим ошибки в передаваемой величине в обоих случаях равно 2* 1, различие состоит лишь в знаке этой ошибки. Поэтому стоимсть потерь при приеме символа k-го разряда в обоих случаях может быть принята одинаковой С10 = С0к\ Правильному же приему символа можно приписать нулевые потери С () = С^к) = 0. Тогда минимизация среднего риска R сведется к минимизации среднего числа ошибок в приеме символов каждого разряда независимо от характера этих ошибок. Критерий минимума среднего числа ошибок был назван В. А. Котельниковым критерием идеального наблюдателя (здесь под идеальным понимается наблюдатель, беспристрастно фиксирующий любые ошибки). Иногда этот критерий называют еще критерием Котельникова.

Допустим теперь, что передаваемая цифровым кодом случайная величина с равной вероятностью может принимать любое значение от 0 до umax. В этом случае вероятности передачи в каждом из разрядов символов 0 и 1 одинаковые: Р0№) = Р*к) = 1/2

Глава 3. Статистическая теория обнаружения сигналов

При указанных условиях по формуле (3.16) получим Т1 = 1,а1пт1 = 0и критерий оптимального обнаружения символа любого разряда на фоне белого шума согласно (3.22) принимает вид:

X {ty (*) - но <д2 - & (*} (*)]2> (324)

-*=i я°

Найдем теперь вероятности ошибочного приема (трансформации)

символов двоичного кода Poi (прием 1 вместо 0) и Рю (прием 0 вместо 1).

Рассмотрение будем вести для двух случаев передачи символов:

а) двоичный код с пассивным нулем: символ 1 передается сигналом и\ (г), имеющим длительность Г и энергию Е, а символ 0 соответствует отсутствию этого сигнала на интервале длительностью Т [uq (f) = 0];

б) двоичный код с активным нулем: символы 1 и 0 передаются различными сигналами щ (/) и щ (г), имеющими одинаковые длительность Т и энергию

т т

J u2Y(t)dt = J u\{t)dt = E. о о

В первом случае критерий (3.24) принимает вид

m m j

2X У (*) и (*) А/- X и2 (*>

* = 1 Jt =

ИЛИ

Ху( 1(*>Д^т- (325)

4-1 °

где для обозначения гипотез вместо Н\ и Но используются принимаемые оценки 1 и 0.

Вероятность Р<н трансформации нуля в единицу есть вероятность того, что случайная величина Go, соответствующая левой части (3.25) при отсутствии сигнала щ (г) в принятой реализации у (t), т.е. при у (ft) = п (ft), будет больше £72.

Найдем закон распределения случайной величины

G0=]>>(ft) i(ft)A/. (3.26)

Поскольку (3.26) представляет линейное преобразование белого шума, то Go является центрированной случайной величиной с нормальным законом распределения

,(0 ,= -exp(-V), (3.27,

где о2у - дисперсия случайной величины Go;