Относительную погрешность, возникающую при усечении спектра сигнала, будем характеризовать отношением среднего квадрата искажения сигнала к его средней мощности 9>с. Тогда получим ее оценку в виде:

< М = АН (1 32)

т.е. относительная погрешность меньше относительной энергии АЕ/ЕС, соответствующей неучитываемой части спектра.

Число дискретных отсчетов, минимально необходимых для задания сигнала длительностью Г при ограничении его спектра частотой 9ь и

9ьТ \9 равно

В = (Г/ДО + 1 = Г2£ь +1 22ЬГ. (1.33)

При этом сигнал приближенно, с погрешностью, определяемой неравенствами (1.31), (1.32), представляется суммой

и{±и{Ш)Щ^Ш. (1.34)

Величину В называют числом степеней свобода или базой сигнала.

Теорема Котельникова указывает на симметрию свойств временного и спектрального (частотного) представлений сигнала: как сигнал, ограниченный во времени, может быть задан дискретным набором его спектральных составляющих (дискретным частотным спектром), так и сигнал с ограниченным спектром мржет быть задан набором его отсчетов в дискретные моменты времени (дискретным временным спектром ). Эта симметрия обоих представлений отображается разложениями (1.10) и (1.21).

Теорема Котельникова имеет фундаментальное значение в теории информации, статистической радиотехнике и ряде других прикладных наук. Вместе с тем она находит и прямое применение при решении практических задач (выбор частоты опроса телеметрических систем, определение режимов работы систем с адаптацией и т.д.). Следует отметить, что разложение Котельникова является не единственным и не всегда лучшим способом интерполяции значений непрерывной функции по ее дискретным отсчетам.

Глава 1. Общие сведения о сигналах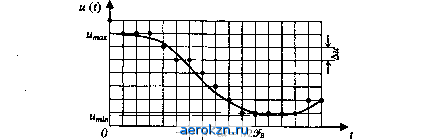

Рис. 1.5

Рассмотрим теперь дискретизацию значений сигнала (квантования сигнала по уровню) для перехода к цифровой форме. Дискретизация значений сводится к замене бесконечного множества возможных значений непрерывного сигнала конечным множеством дискретных его значений. Для этого весь интервал от umin до итах возможных значений сигнала разбивается на конечное число дискретных уровней (рис. 1.5) с интервалом между уровнями (шагом квантования) Ди. Значения и if) сигнала в дискретные моменты отсчета tk заменяются ближайшим дискретным значением щ в соответствии с правилом

где

- целая часть величины, стоящей в скобках.

На Рис. 1.5 дискретные значения сигнала обозначены точками. Легко видеть, что погрешность при таком представлении ( шум квантования ) не превышает половины шага квантования Дм.

При малом Д„, когда распределение возможных значений сигнала в пределах шага квантования можно считать равномерным, среднеквадра-тическое значение этой погрешности [16].

а* = Ди/2л/Т.

(1.35)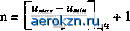

(1.36)

Таким образом, непрерывный сигнал и (г) может быть преобразован в цифровой. Погрешности, вносимые при таком преобразовании, определяемые формулами (1.31) и (1.35), могут быть уменьшены до требуемой величины соответствующим выбором шага квантования по времени и по уровню.

Глава 2

СЛУЧАЙНЫЕ СОБЫТИЯ, ВЕЛИЧИНА, ФУНКЦИЯ И ИХ ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ

2.1. Случайное событие и вероятность

Под случайными событиями понимаются события, которые могут произойти или не произойти в результате данного опыта. Если при -кратном повторении какого-либо опыта относительное число появлений j-ro события по мере увеличения общего числа реализаций этого опыта N стремится к некоторому пределу

Pi = \im(ni/N), (2.1)

то говорят о статистической устойчивости результатов данного опыта.

Числа Р/, позволяющие при этом количественно сравнить события по степени их возможности, называются вероятностями этих событий. Чем чаще имеет место данный исход опыта, тем больше его вероятность. Достоверное событие, которое непременно должно произойти при каждом испытании, имеет максимально возможное значение вероятности Р,- = 1. В противоположность ему невозможное событие, т.е. событие, которое в данном опыте не может произойти, имеет минимальное значение вероятности Pi - 0. Для всех остальных событий, которые могут иметь место при данном опыте, но не при каждом его повторении, вероятность лежит в пределах 0 < Р,< 1.

Для некоторых опытов вероятности отдельных исходов могут быть предсказаны умозрительно на основе анализа условий опыта. Это, как правило, те случаи, когда можно выделить такие элементарные исходы опыта, ни одному из которых нельзя отдать предпочтение, так что все они должны приниматься равновероятными. Так, например, при бросании монеты нет никаких оснований отдать предпочтение одному из двух возможных исходов опыта (падение монеты гербом вверх или вниз) и обоим им должна приписываться одинаковая вероятность, равная 1/2. То же относится и к бросанию игральной кости в виде идеального кубика, когда любая из его граней с одинаковой вероятностью Р, = 1/6 может оказаться

При заданной величине допустимой ошибки квантования Ьи** = их -- и (tk) (заданной величине о* и соответственно при заданном шаге квантования Ам = 2 VTo*) требуемое число уровней квантования

верхней. Нет оснований отдать предпочтение и какой-либо из игральных карт при их сдаче из хорошо перетасованной колоды и т.д.

В более сложных случаях, когда не удается умозрительно определить вероятности элементарных исходов опыта, единственным методом их определения остается непосредственный подсчет относительной частости появления отдельных исходов при многократном воспроизведении опыта. В этом случае опыт одновременно позволяет убедиться в статистической устойчивости его результатов и найти вероятности отдельных исходов.

В большинстве случаев, представляющих практический интерес, мы сталкиваемся со сложными событиями, представляющими определенные сочетания исходов ряда элементарных опытов. Прибегать для оценки вероятности такого сложного события каждый раз к опыту чрезвычайно трудно, а иногда и просто невозможно (например, при проектировании, когда объект испытаний вообще отсутствует). Возникает задача косвенной оценки вероятности сложных событий через известные вероятности /других событий, логически с ними связанных. Систему таких косвенных методов оценки вероятностей, позволяющих свести к минимуму экспериментальные оценки, дает теория вероятностей.

Введем некоторые понятия, являющиеся основополагающими для теории вероятностей.

События называются несовместными в данном опыте, если никакие два из них не могут появиться вместе. Если в результате каждой конкретной реализации опыта обязательно должно появиться хотя бы одно из событий Aj, А2, Ал, то такая группа событий называется полной. Противоположными называются /два несовместных события А и лГ, образующих полную группу. События называются независимыми, если вероятность появления одного из них не зависит от того, имело место или нет другое из этих событий. Если же вероятность события А зависит от того, имело ли место событие В, то такие события называются зависимыми. В этом случае можно ввести условную вероятность Р (А\В), представляющую вероятность события А при условии,что имело место событие В.

Суммой нескольких событий называется событие, заключающееся в появлении хотя бы одного из них. Произведением нескольких событий называется событие, заключающееся в совместном появлении всех этих событий. Понятия суммы и произведения употребляются здесь не в арифметическом смысле, а обозначают соответствующие логические операции.

В основе косвенных методов оценки вероятностей лежат теоремы сложения и умножения вероятностей.

Теорема сложения вероятностей: вероятность суммы несовместных событий Аи А2, А„ равна сумме вероятностей этих событий:

Р(АЬ + А2, + ...+ А„) =Х P(Aj). (2.2)

1 = 1

Справедливость равенства (2.2) вытекает из того, что в случае несовместных событий число исходов опыта, при которых имеет место любое из событий Аи А2, Ап будет равно сумме исходов, отвечающих каждому из них. Следует еще раз отметить, что равенство (2.2) справедливо только для несовместных событий.

Теорема умножения вероятностей: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, соответствующую условию, что имело место первое событие:

Р(АВ) = Р(А)Р(В\А). (2.3)

В справедливости (2.3) легко убедиться, сопоставляя соответствующие числа исходов опыта. Действительно, если в N опытах п раз происходило событие А и при этих п исходах к раз одновременно имело место и событие В, то при неограниченном возрастании числа опытов N и соответственно исходов А имеем:

P(A) = lim(n/7V), Р(Я|А) = Нт(Ш).

Поскольку из общего числа N опытов только в к случаях имели место одновременно события А и В, то получим:

Р(АЯ) = 11т(Ш) = Ит =Р(А)Р(В\А).

Вероятность произведения двух событий можно также записать в виде

Р(АВ) = Р(В)Р(А\В). (2.4)

Из (2.3) и (2.4) получаем

рт. рщрЩ1 (25)

В частном случае, если события А и В независимы, Р (В\А) = Р (В) и

Р(АВ) = Р(А)Р(В).

(2.6)

Проиллюстрируем применение теорем сложения и умножения вероятностей на простейших примерах.

Найдем вероятность того, что из хорошо перетасованной колоды, содержащей 36 карт, будет вытащена карта данной масти. В данном случае требуется найти вероятность суммы 9 несовместных равновероятных событий, заключающихся в вытаскивании одной из карт данной масти, вероятность каждого из которых равна 1/36. Следовательно, согласно теореме сложения искомая вероятность Р = 9(1/36) = 1/4.

Найдем теперь вероятность сложного события, заключающегося в том, что из урны, содержащей 7 красных и 3 белых шара, неотличимых на ощупь, в двух попытках будут вынуты 1 красный и 1 белый шар.

Рассмотрим сначала случай, когда перед очередной попыткой вынутый ранее шар возвращается в урну. В этом случае результаты обеих попыток представляют независимые события. Поскольку вероятность вынуть любой из 10 шаров в каждой попытке равна 1/10, то в соответствии с теоремой сложения красный шар может быть вынут с вероятностью 7/10, а белый - с вероятностью 3/10. Вероятность вынуть в двух независимых попытках разноцветные шары в любой последовательности

Рр = Р (кб + бк) = Р (кб) + Р (бк) =

= Р (к) Р (б) + р (б) Р (к) = 0,70,3 + 0,30,7 = 0,42.

Здесь обозначения событий кб и бк соответствуют последовательности, в которой вынимаются красный (к) и белый (б) шары.

В случае, когда шар, вынутый в первой попытке, в урну не возвращается, вероятность того или иного исхода во второй попытке зависит от результатов первой попытки. Если в первой попытке был вынут белый шар, то условные вероятности вынуть при второй попытке из урны, содержащей 7 красных и 2 белых шара, красный или белый шар соответственно равны

Р(к|6) = 7/9, Р(б|к) = 2/9.

Бели же в первой попытке был вынут красный шар, то условные вероятности вынуть красный или белый шар во второй попытке соответственно равны

Р (к|к) - 679 - 2/3, Р (б|к) - 3/9 - 1/3.

Вероятность вынуть в двух попытках разноцветные шары

РРшш = Р (к) Р (б|к) + Р (б) Р (к|б) = 0,7(1/3) + 0,3(7/9) = 0,467.

Пользуясь теоремами сложения и умножения вероятностей, получим некоторые формулы,которые нам потребуются для последующего изложения материала.

Найдем вероятность Рп того, что при п независимых испытаниях, исходом которых может быть одно из двух противоположных событий А или А, событие А произойдет ровно к раз.

Вероятность события А обозначим Р (А) = Р, тогда Р(А) = 1-Р. Вероятность конкретной комбинации исходов п независимых испытаний, когда при определенных к испытаниях появилось событие А, а при остальных п-к испытаниях - событие А, в соответствии с теоремой умножения вероятностей равна Р*(1-Р) л~*, независимо от того, в каком порядке чередовались в данной комбинации исходы событий АиА. Интересующее нас сложное событие представляет сумму всех исходов n-кратных испытаний,

дающих к появлений события А. Поскольку исходы с разным порядком чередования событий А и А несовместны, а число исходов, дающих в разной последовательности к появлений события А в N испытаниях, равно числу сочетаний из п элементов по к, то в соответствии с теоремой сложения вероятностей

Pn.k = C\Pk(\-P)n-\ (2.7)

где

гк - п* с Л~ к\(п-к)\

число сочетаний из п элементов по к.

Формула (2.7) носит название биномиального закона.

Рассмотрим теперь две группы зависимых событий Ль А2, Ап и Ви 1?2, Вп каждая из которых составляет полную группу несовместных событий. В этом случае полная вероятность события, т.е. вероятность того, что событие Л,- вообще произойдет совместно с любым из событий Bt равна

Р(Ад= Хр(А,) = Хр(Ву)Р(А,В;). (2.8)

j= 1 j= i

На основании формул (2.5) и (2.8) получим

ГШ- Р-ЧШ - r,)fW,) <м>

2>(Я/)Р(А,Д,)

Формула (2.9) носит название формулы Байеса и позволяет определить условные вероятности Р (В/А/), характеризующие правдоподобность той или иной гипотезы об исходе непосредственно не наблюдаемого явления В при известном исходе явления А, если только известны значения вероятностей Р (Bj) исходов Bj (в сочетании с любым из исходов А,) и значения условных вероятностей Р (Ai\Bj).

2.2. Случайные величины и их вероятностные Характеристики

Если случайная величина может принимать конечное число дискретных значений xh исчерпывающей вероятностной характеристикой ее служит распределение вероятностей этих значений Р,. (По аналогии со случайными функциями случайные величины обозначим буквами

греческого алфавита, а их конкретные реализации - буквами латинского алфавита).

Если случайная величина J; непрерывна и может принимать любое значение на интервале [jtmin, *max], то ее статистической характеристикой может служить так называемый интегральный закон распределения F(x)=P (£< jc), определяющий вероятность того, что случайная величина {; не превзойдет значение х. Из определения интегрального закона распределения вытекает следующее очевидное соотношение:

Р х2) = F(x2) -F(*i) (2.10)

где Р (х\£>< х2) - вероятность того, что случайная величина не выйдет за пределы интервала [хи х2].

Очевидны следующие свойства функции F(x): F(x) - монотонная неубывающая функция;

F(-oo) = 0, F(+oo) = l.

Если функция F (х) дифференцируемая, то в качестве вероятностной характеристики случайной величины удобно использовать дифференциальный закон распределения или закон распределения плотности вероятности

w(x) = dF(x)/dx (2.11)

Очевидны следующие соотношения:

F{x) = jw(x)dx; jw(x)dx=l;

P(xx x2) = jw (x)dx.

Помимо законов распределения, часто используются числовые характеристики случайных величин, так называемые моменты распределения. Моменты, характеризующие распределение случайных величин относительно нуля, называются начальными.

Для непрерывных случайных величин начальный момент k-го порядка определяется по формуле

Щ*©= J xkw(x)dx. (2.12)

При этом предполагается, что несобственный интеграл (2.12) абсолютно сходится, т.е.

]\x\kw(x)dx

имеет конечное значение.

. Для дискретной случайной величины принимающей значения *ь x2f ...>хпс вероятностями Р\,Р2, ..., Р„,

= Х^гРг. (2.13)

Наиболее важное значение имеют моменты 1-го и 2-го порядков. Начальный момент 1-го порядка дает математическое ожидание или среднее значение случайной величины £:

*ii©= ]xw{x)dx. (2.14)

Разность = £; - mi(£) называется отклонением случайной величины. Моменты распределения отклонений случайной величины называются центральными и обозначаются Мк (£). Нетрудно убедиться, что М\ (£) = 0.

Случайные величины с нулевым средним значением называются центрированными. Любые случайные величины можно свести к центрированным, если перейти к отклонениям А^.

Начальный момент 2-го порядка определяет средний квадрат случайной величины {;:

т2 © = ]x2w(x)dx. (2.15)

Центральный момент 2-го порядка называется дисперсией случайной величины:

М2£) = о\ = ][xmim1w{x)dx. (2.16)

Дисперсия характеризует разброс случайной величины относительно ее среднего значения.

Величина о^ = V М2 (£) называется среднеквадратическим или стандартным отклонением случайной величины от ее среднего значения.

Отношение А^/а^ называется нормированным отклонением случайной величины.

Центральный и начальный момент 2-го порядка случайной величины связаны простым соотношением:

M2© = m2(-m21(). (2.17)

Если закон распределения случайной величины симметричен относительно ее среднего значения, т.е. w (т\ + х) = w(m\ -х), то центральный момент 3-го порядка такой случайной величины равен нулю:

j(x-mtf w(x)dx= jy3w (mi + у) dy = О,

так как y3w (т\ +у) - нечетная функция у.

Отличие от нуля центрального момента 3-го порядка характеризует асимметрию закона распределения. Безразмерный коэффициент

называют коэффициентом асимметрии.

Для совокупности двух случайных величин £i и £2 исчерпывающей вероятностной характеристикой служит двумерный интегральный закон распределения F (хь х2) = Р (£i< хх, £2< х2), определяющий вероятность того, что случайные величины £i и £2 не превосходят соответственно значений хх и хъ Если функция F (jcb х2) дифференцируемая, то вероятностной характеристикой двумерной случайной величины может служить двумерный дифференциальный закон распределения или двумерная функция распределения w2 (хь х2) = d2F (хи х2)/дх\дх2. Аналогично могут быть введены многомерный интегральный закон распределения и многомерные функции распределения для совокупностей из любого числа случайных величин.

Можно также ввести числовые характеристики для совокупности двух случайных величин £i и £2, имеющих двумерную функцию распределения и>2 (хь х2). Весьма важной числовой характеристикой совокупности двух случайных величин является смешанный второй центральный момент или ковариация случайных величин и £2:

М2 ($ь Ы = J J [xi - m,(£i)] [x2 - яц(§2)] w2 (хь x2) x

xdx\dx2= J J x\x2w2(xux2)dx\dx2-mi(£i)mi(£2). (2.18)

Если случайные величины £i и независимы, то w2(xu*2) = = w (jci) w (х2), и двукратный интеграл в (2.18) распадается на произведение двух однократных интегралов:

J jciw (xi) dxi = mi(), j x2w (xi) dx2 = mife)

и, следовательно, М2(£ь ) = 0. Поэтому ковариация М2(£ь{;2) может служить некоторой.мерой зависимости между двумя случайными величинами. Чаще в качестве такой меры принимают безразмерный коэффициент корреляции

9ЬМ = Мг fti. Ь) / Vi) М2£2).

Две случайные величины, для которых коэффициент корреляции равен нулю, называются некоррелированными. Случайные величины, для которых 1-й начальный момент их произведения

*i№) = o,

называют ортогональными. Если средние значения случайных величин равны нулю, то понятия ортогональности и некоррелированности случайных величин совпадают.

, Моменты распределения того или иного порядка, являясь важными числовыми характеристиками случайной величины, не являются, однако, их однозначной полной статистической характеристикой: случайные величины, имеющие одинаковые 1-й и 2-й моменты, могут иметь разные законы распределения.

2.3. Нормальный закон распределения

Среди случайных величин особое место занимают нормальные случайные величины, подчиняющиеся так называемому нормальному закону распределения:

~згЧ-%£]- (2Л

Определим 1-й начальный момент нормальной случайной вели-тары£:

Сделав замену (jc - a) IV2 а = у, получим

тх® = Щ- ]yc~y2dy+ * h-y2dy = a,

ш*йс первый из интегралов равен нулю в силу нечетности подынте-гршьйЬй функции, а

/е- = л/Т [34].

Итак, a = mi (£).

Определим теперь 2-й центральный момент нормальной случайной величины

мг®=>-а>2ехр[-1]л=

так как

J/e->Jrfy=[34].

Таким образом, величины а и о , полностью определяющие нормальный закон распределения, представляют собой соответственно среднее значение и дисперсию случайной величины т.е. нормальный закон распределения полностью определяется, если известны первые два момента. Из формулы (2.19) видно, что нормальное распределение симметрично относительно среднего значения случайной величины а, т.е. 3-й центральный момент и все центральные моменты нечетного порядка равны нулю. Максимум плотности вероятности, соответствующий х = а, равен

с = w (а) = I/oVItT.

На рис. 2.1 приведен вид нормального закона для различных а при а = 0.

w(x)

а1<а2<а3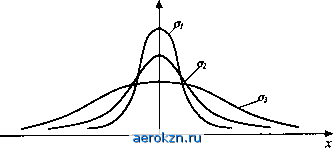

Рис. 2.1

Нормальный закон распределения занимает особое положение в силу того, что большинство реальных случайных величин имеет распределение, близкое к нормальному. Последнее обстоятельство связано с тем, что

на практике случайные величины обычно являются результатом совокупного действия многих независимых случайных факторов и, при некоторых условиях, по мере увеличения числа этих факторов закон распределения асимптотически приближается к нормальному. Условия эти определяются центральной предельной теоремой теории вероятности, которая в упрощенном виде может быть сформулирована следующим образом [1]: если независимые случайные величины £ь^2, £л имеют одинаковые распределения с конечной, отличной от нуля дисперсией а2, то при л-* сумма этих величин стремится к нормальному распределению со средним значением

Я£ = X Wi (£*)

* = 1

и дисперсией <j\ = па2.

А.М. Ляпунов показал [36], что тенденция к нормализации суммы Случайных величин имеет место и при более общих предположениях.

Рйс 2.2

Решение многих практических задач не столь критично к точности аппроксимации закона распределения и уже в случае, когда случайная величина определяется несколькими примерно равноценными независимыми случайными факторами, закон ее распределения можно приближенно аппроксимировать нормальным законом.

Интегральный закон распределения, соответствующий нормальному закону (2.19), имеет вид:

f х

F(*) = \w(y)dy = -]= fexp о V 2л; i

Если перейти к нормированным отклонениям (х - а)/о, то получим

Функция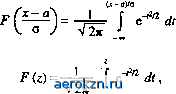

(2.21)

представляющая собой вероятность того, что нормированное случайное отклонение не превзойдет величину z, называется интегралом вероятности. Вид этой функции приведен на рис. 2.2. Поскольку

то F(-z) = 1 -F(z) и функцию F(z) достаточно определить в положительной области.

Вероятность того, что нормальная случайная величина £ не выйдет за пределы интервала [jcb х2]

P(Xlx2)F-Fj. (2.22)

2.4. Случайные функции и их вероятностное описание

Случайные функции так же,как и случайные величины, должны определяться вероятностными законами распределения их реализаций. Каждая реализация случайной функции £ (г) представляет функцию времени х\ (t). Если на спектр случайного сигнала не наложить никаких ограничений, то его реализации даже при конечной их длительности будут определяться бесконечным числом координат, представляющих значения функции x{ (t) в различные моменты времени. Вероятностное описание такой случайной функции эквивалентно вероятностному описанию бесконечномерной случайной величины и соответственно требует использования бесконечномерных законов распределения.

Задача описания случайной функции значительно упрощается, если ширину ее спектра ограничить сверху величиной В этом случае каждая реализация случайной функции длительностью Т в соответствии с теоремой Котельникова полностью определяется дискретной выборкой, содержащей N = 2&ВТ отсчетов, следующих с интервалом At = 1/2&в. Такая случайная функция может быть задана N-мерным дифференциальным законом распределения, определяющим плотность вероятности

wn(xu x2j xN) ее реализации, характеризуемой совокупностью значений Хи х2, ...,xnb дискретных точках отсчета.

Вероятность того, что осуществится реализация, значения которой в дискретных точках отсчета лежат в пределах (хх, х\ + dx\\ (xn, xn + dxN\ равна wn(xu x2, xN)dxudx2 ... dxN.

Заменяя непрерывные реализации jc{ (0 N-мерной дискретной выборкой, мы тем самым все реализации, имеющие одинаковый спектр до некоторой граничной частоты &ш и отличающиеся лишь высокочастотными составляющими спектра за этой границей, заменяем некоторой средней реализацией, соответствующей усечению спектров верхней границей Уш. Среднеквадратическая ошибка представления всех этих реализаций общей N-мерной выборкой согласно (1.31) не превосходит V АЕ/Т, где АЕ - энергия, приходящаяся на часть спектра реализаций, лежащую выше границы Выбор размерности закона распределения wN(x\, х2, ...,*#), характеризующего случайную функцию £ (О, зависит от требований к точности представления ее реализаций. Чем меньше размерность N закона распределения (чем меньшей выбрана граничная частота #,), тем больше величина АЕ/Т, характеризующая погрешность представления реализаций случайной функции данной выборкой. И, наоборот, чем больше размерность N закона распределения, тем выше точность представления реализации случайного сигнала.

2.5. Корреляционные характеристики случайных процессов. Стационарные и эргодические случайные процессы

При рассмотрении случайных величин наряду с законами распределения весьма полезными оказались некоторые числовые характеристики (среднее значение, дисперсия и др.), представляющие детерминированные величины. При рассмотрении случайных процессов аналогичную роль играют детерминированные функции, дающие те же числовые характеристики случайных величин, представляющих значения этих процессов в соответствующих временных сечениях. К числу таких характеристик относятся среднее значение, дисперсия, корреляционная функция случайного процесса и др. Среднее значение или первый начальный момент случайного процесса £ (г) представляет функцию времени

a(t) = mi {£(*)} = \ xw\(x\t)dx,

(2.23)

где xw 1 (jc; t) - одномерное распределение случайной величины, представляющей возможные значения случайного процесса £(f) в фиксированный момент времени t. Дисперсия случайного процесса £ (г) или 2-й центральный момент также представляет функцию времени

a\ = m1{KW-a4(r)]2}= ][x-a%(t)f wx (г, t)dx. (2.24)

Корреляционная функция случайного процесса или смешанный 2-й начальный момент представляет двумерную функцию времени

= j jxix2w2 (хи х2\ tu h) dxxdx2, (2.25)

где w2 (jci, x2, tu h) - двумерное распределение случайных величин £ (t{) и £ (t2), представляющих возможные значения случайного сигнала (г) для временных сечений t\ и t2. Часто вместо случайного процесса рассматривают его флюктуации - отклонения от среднего значения

So(f) = 5()-at(r). (2.26)

Нетрудно видеть, что а^ (t) = 0, а о\ (г) = а\ (t). Корреляционная функция флюктуации случайного процесса носит название ковариационной функции и имеет вид

% (tu h) = mi {К (h) - at № К fa) - <Ц (fe)] 1. (2.27)

Из (2.27) и (2.24) следует, что

a\(t) = B(t,t),

т.е. дисперсия представляет значение ковариационной функции В^ (tu h) при равенстве аргументов t\ и t2.

Случайный процесс £ (t) называется строго стационарным или стационарным в узком смысле , если его функция распределения w (jci, ль,.... хп\ tub -* *п) произвольного порядка п не меняется при любом сдвиге всей группы точек гь h tn, т.е. при соблюдении для любых п и т условия:

wn (хи хъ хп\ tu h О = wn (хи хъ хп\ fj+x, Г2+х гл+х) (2.28)

Из (2.28) следует, что двумерна функция распределения стационарного процесса зависит только от интервала i-t2-t\ между точками отсчета:

и>2 (*ь х2; tu h) = w2 (хи х2\ т), (2.29)

а одномерная функция распределения w\ (х) не зависит от временного сечения.

Соответственно для стационарного случайного процесса от начала отсчета времени не зависят и введенные статистические характеристики

а$ (t) = a$ = const; (2.30)

(t) = c\ = const; (2.31)

B% (r, t + x) = B% (t) = j j Xlx2w2 (xlt x2; x) dxxdx2 (2.32)

Следует заметить, что условие (2.29) и вытекающие из него условия (2.30) - (2.32) являются необходимыми, но недостаточными условиями строгой стационарности случайного процесса, ибо независимость от начала отсчета времени двумерной функции распределения еще не гарантирует соблюдение этого же условия и для всех распределений более высокого порядка. Однако для большого числа практических задач оказывается достаточным знание свойств процессов, определяемых первыми двумя моментами. Раздел теории, посвященный изучению этих свойств, называется корреляционной теорией. В рамках корреляционной теории процессы, удовлетворяющие условию (2.29), ничем не отличаются по своим свойствам от строго стационарных. Случайные процессы, удовлетворяющие этому условию, получили название стационарных в широком смысле (или в смысле Хинчина).

В данной книге в основном мы будем рассматривать именно такие процессы и будем называть их для краткости просто стационарными.

Корреляционная и ковариационная функции стационарного случайного процесса, описываемого действительной функцией времени, обладают следующими свойствами**:

1) являются четными функциями аргумента х

, , Сс)=Д$(-т); Яь(т) = Вь(-т);

Случайные процессы, описываемые комплексными функциями времени, здесь не рассматриваются.

2) при т = 0 имеют максимальное значение, равное соответственно

2 2 2

3) при т - °° 2%- а|, аЯ-0.

Нормированной корреляционной функцией называется функция Вф)-а\ = (х) * ВЬ(0)

Очевидно, что р^ (0) = 1 и р^ (°°) = 0.

Из последнего условия следует, что для стационарного случайного процесса, как правило, можно выбрать такое значение то, что при т>то корреляцией между отсчетами процесса можно пренебречь.

Поскольку максимальное значение р^ (т) равно 1, то в качестве меры скорости спада р^ (т), т.е. меры интервала то, при значительном превышении которого можно не считаться с корреляцией между отсчетами, можно использовать площадь под кривой р^ (х), приняв

хо= JlftWI*.

(2.34)

(Практически корреляцией можно пренебречь уже при т^(3-4)то). Величина То определяемая формулой (2.34), называется интервалом корреляции. Геометрически интервал корреляции может интерпретироваться как половина ширины прямоугольника единичной высоты, площадь которого равновелика площади, ограничиваемой кривой р^ (т) (рис. 2.3).

о

Рис. 2.3

До сих пор мы рассматривали статистические характеристики, получаемые осреднением по множеству реализаций. Рассмотрим теперь некоторые числовые характеристики, получаемые осреднением тех же величин по времени для реализаций большой длительности. Осреднение по времени будем обозначать скобками вида ( ). Временное среднее r-й реализации

т

(xr(t)) = lim±- jxr(t)dt (2.35)

можно трактовать как постоянную составляющую реализации. Средний по времени квадрат реализации

г

<x2r(r)> = lim-L J д?г (i) А (2.36)

можно трактовать как среднюю мощность реализации (представляя реализацию как изменение тока или напряжения на нагрузке 1 Ом). Можно ввести функцию временной корреляции

г

(xr(t)xr(t + T)) = lim±- \ xMxti + x)dt. (2.37)

В общем случае для произвольного случайного процесса эти числовые характеристики имеют для разных реализаций различное значение и поэтому не имеют смысла как статистические характеристики процесса. Исключение составляют эргодические случайные процессы.

Случайный процесс называется эргодическим, если любая его статистическая характеристика, полученная усреднением по множеству возможных реализаций, с вероятностью, сколь угодно близкой к едини-це,равна соответствующему временному среднему, полученному на достаточно большом интервале времени из одной единственной реализации случайного процесса. Эргодичность случайного процесса предполагает его стационарность, но не наоборот: стационарный процесс может не быть эргодическим. Например, случайный процесс вида

£ (0 = £о (0 + П (2.38)

где £о (0 - эргодический случайный процесс; tj - случайная величина, Меняющаяся от реализации к реализации, будет стационарным, но не эргодическим (его числовые характеристики, полученные осреднением по времени, меняются от реализации к реализации из-за изменения г|).

Строгая эргодичность означает, что множество реализаций данного случайного процесса на некотором конечном отрезке времени характеризуется теми же многомерными законами распределения любого порядка, что и множество отрезков этого процесса той же длительности, нарезанных из одной бесконечно длинной реализации. Наряду с понятием строгой эргодичности по отношению ко всем возможным вероятностным Характеристикам случайного процесса могут использоваться частные определения эргодичности, относящиеся к отдельным характеристикам (эргодичность по флюктуациям случайного процесса, дисперсии и т. д.).