определения значений Fi{x) при произвольных значениях параметров а и а>0, если заметить, что из (2.67) и (2.68) следует

(2.69)

Таблицы интеграла Лапласа составлены для положительных аргументов, а значения F{-х) определяются из очевидного соотношения 1

F{x)+F{-x) = l. (2.70)

Вблизи начала координат функция F{x) имеет участок, близкий к линейному, который хорошо описывается несколькими пер-зыми членами степенного ряда

40 336

2-1(2/?- 1)!

(2.70а)

При достаточно большом аргументе имеет место асимптотическое разложение

\ j j 3

Fix) = 1-

л

1+ S(-l)

(2.706)

Заметим, что если в знакопеременном ряде ограничиться несколькими членами, то ошибка будет меньше значения первого отброшенного члена. Поэтому из (2.706) следует

На рис. 2.5 для сравнения приведены функции нормального распределения при тех же значениях ст, что и на рис. 2.4. Предельная кривая при а->0 имеет вид единичного скачка в точке х=а.

Часто вместо функции F(x) рассматривается и табулируется так называемый интеграл вероятности (функция ошибок, функция Крампа)

Ф(jc) = fехр (-z )dz = 2F{хV2) - 1 (2.71а)

к л о

и функция

io W = I ехр ( - f ] = F (x) -i- = -1Ф ( 2). (2.716)

* Заметим, что формула (2.70) верна для любой случайной величины, если ее плотность вероятности симметрична относительно нуля.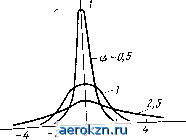

Рис. 2.4. Плотности нормального распределения при различных дисперсиях

Рис. 2.5. Функции нормального распределения при различных дисперсиях

ДЛЯ которой (2.70) переходит в более простое соотношение

Fo{-x)=-Fo{x). (2.71b)

2.4.3. Совокупность независимых гауссовских случайных величин. Если 1и - у In - совокупность независимых гауссовских случайных величин с параметрами

то из (2.43) и (2.66) следует, что совместная плотность вероятности этой совокупности случайных величин

ехр

(2.72)

(2я) /21...п

Формула (2.72) является частным случаем общей формулы {2.65) (при iift=Sjfe), для которого Dik=&ik, бгй=1 при i=k 6 fe=0 при Ковариационная матрица Kg и обратная ей мат-

рица К~Ч в этом случае диагональные.

Сравнение формул (2.65) и (2.72) показывает, что из попарной некоррелированности гауссовских случайных величин следует их независимость. Это положение является важным исключением общего утверждения о том, что из некорреллированности случайных величин не следует их независимость, и является характерной особенностью нормального распределения вероятностей.

2.4.4. Совокупность двух зависимых гауссовских случайных величин. Двумерная плотность двух зависимых гауссовских величин li и 2 зависит от пяти параметров: а аг, си 02, Ri,i, =г. Детерминант

1 г г 1

= 1-Л

а алгебраические дополнения Dii=Z)22=l, /)i2=£>2i=-г. Из 2* 35

(2.65) при п=2 находим двумерную плотность вероятности двух гауссовских случайных величин (рис. 2.6)

2jiaia2 Vl -л2

ехр

2(1~л^)

(i- i)

(2.73)

Функция распределения двух гауссовских случайных величин Р^лЛъ 2) =

= ,1 Х Т -Р { - 1 dudv. (2.73а)

в частном случае при

= h функция \Fii, {хих2)

связана простым соотношением с табулированным интегралом (см. Приложение 1 в [1])

/ , ч 1 7 7 с Ги - 2ruv + у2

dudv.

(2.736)

Условная плотность гауссовской случайной величины 2 при условии, что зависимая от нее гауссовская случайная величина = = Хи в соответствии с (2.55), (2.66) и (2.73) равна

w{x\X:,) =

г ехр

2а2(1-г2)

(2.74)

Из (2.74) следует, что условная плотность описывается функцией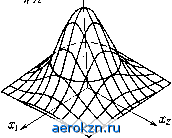

Рис. 2.6. Двумерная плотность Рис. 2.7. Условные плотности нормального нормального распределения распределения

нормальной плотности вероятности с параметрами: условное среднее значение

rni {ЬI =а2+г (xi-ai) огМ (2.75а)

и условная дисперсия

\X2{b\xi}=o2{l-n, (2.756)

При г=0, что соответствует независимости случайных величин Si и I2, условная плотность (2.74) переходит в плотность вероятности случайной величины 2- При

wixM8[---V (2-76)

На рис. 2.7 согласно (2.74) построены кривые условных плотностей нормального распределения при Xi=ai+3oi и нескольких значениях параметра г.

2.5. ортогональное разложение плотностей вероятности

2.5.1. Разложение в ряд по ортогональным полиномам. В некоторых случаях полезно аппроксимировать плотность вероятности случайной величины частичной суммой ряда, представляющего разложение функции плотности по ортогональным функциям. В качестве весовой функции ф(х), которая определяет совокупность ортогональных функций {Qn(x)}y выбирают какую-нибудь простую, известную плотность вероятности, которая приближенно отражает основные свойства аппроксимируемой плотности. Формально упомянутый ряд, представляющий произвольную плотность вероятности w{x), можно записать следующим образом:

wi(x)=={x)i сМх). (2.77)

Коэффициенты Ck можно определить, умножив обе части (2.77) на функцию Qn{x) и проинтегрировав с использованием условия ортогональности

]vix)Qu{x)Qn{x)dx = 8, (2.78)

где

Sftn

- символ Кронекера.

При этом в сумме все члены, за исключением одного при k= ~Пу равны нулю и, следовательно^

]wi{x)Qn{x)dx, (2.80)

Если {QnW} - совокупность ортогональных полиномов, та Qn{x)= 2 urX . Тогда

Cn=S r/n (2.81)

где Шг-момент г-го порядка случайной величины g и, следовательно,

Щ W = Ф W 2 2 Qfe () /п„ (2.82)

конечно, при условии, что моменты гпг случайной величины существуют.

Сходимость ряда (2.82) необходимо установить в каждом конкретном случае. Однако существуют задачи, в которых сходимость указанного ряда не имеет значения. Речь идет о построении аппроксимации неизвестной функции распределения, если заданы лишь несколько моментов этого распределения. Поэтому важно быть уверенным, что первые слагаемые ряда (2.82) дают достаточно хорошее приближение к (х). Тогда вопросами сходимости можно и не интересоваться. Ряд (2.82) может быть даже расходящимся, моменты более высокого порядка могут вовсе не существовать, а аппроксимация несколькими первыми слагаемыми может оказаться лучшей, чем в том случае, когда указанный ряд сходится.

2.5.2. Разложение по полиномам Эрмита. Чтобы не усложнять выражений, предположим, что wix) представляет плотность нормированной случайной величины с нулевым средним и единичной дисперсией. Переход к распределению с произвольными средним

а и дисперсией дает (/

Начнем с разложения в ряд по полиномам Эрмита:

fin{x) = {- l) expf-)-expf - п = ОАХ,.. (2.83)

\ J dx \ 2 /

В рассматриваемом случае (p(x) = (1/1/2я)ехр (-л:2/2) - нормальная плотность вероятности. Учитывая условие нормировки (2.78), получаем в соответствии с (2.77) (ряд Грама -Шарлье)

Ш5 W = -exp(i Н^х), (2.84)

где

Ck = -]wi (х) {х) dx-тг {Я, т (2.85)

причем со=1, а вследствие принятой нормировки случайной ве-38

личины I имеем Ci = C2=0. Используя определение полиномов Эрмита, можно (2.84) переписать в виде

wi{x)==ipix)+ i (~ 1)г7гФЧ^). (2.86)

где ф^>(л:)-к'Я производная нормальной плотности распределения. Первые несколько коэффициентов Ch в ряду (2.86):

c. = -7Z7 ]{x3x)w{x)dx=, с,= ]{x-6x + 3)w{x)dx-.

У4\ -i V41

С5 = -!:= ?(;c5-10A? + 15jc)oyg(;c)dA:=-4:rf --lOkV (2.87) Уб! Уб! V /

Тогда первые три члена разложения (2.86) представляются следующим образом:

WI {X) = ф (;с) - А ф(3) (;,) + X ф(4) () + ..., (2.88)

где к и 7 -коэффициенты асимметрии и эксцесса распределения случайной величины

Из (2.88) нетрудно также описать аппроксимацию интегральной функции распределения:

Fi{x) F{x)- ф(2) {X) + ф(3) {X)- ..., (2.89)

3! 4!

где F{x) - интеграл Лапласа.

2.5.3. Разложение по полиномам Лаггера. Разложим плотность вероятности случайной величины, принимающей положительные значения, в ряд по полиномам Лаггера

(д^) = ( l) -L е^ {х^+ е-),

п = 0, 1, 2,..., а>~1, >0. (2.90)

В этом случае ц>{х) =xe-/T(a+l), х^О, а>0 (гамма-распределение); учитывая условие нормировки (2.78), получаем в соответствии с (2.77)

где

Cft - (х) Li > {X) dx. 2 .91а)

Так как для неотрицательной случайной величины среднее mi>0, то все ее значения можно нормировать путем деления на гпи Тогда в (2.91) при а = 0

Со = {х) = 1, Ci = J(l - X) wi (x)dx = 0, / у2 \ me - 2m?

ms -9mami + 12mj 6mf

Следовательно, первые члены разложения (2.91) представляются следующим образом:

mj - 9m2mi+ 12mj 6m?

(2.92)

2.5.4. Разложение no полиномам Чебышева. Разложим в ряд плотность вероятности случайной величины, возможные значения которой принадлежат интервалу (-1, 1), по полиномам Чебышева:

7 (;e) = cos(narccos = (x-/i?) l/2,

л=0, 1, 2, .... д:1. (2.93)

В этом случае ф(а:) = [,(1-д;2)*/2я]->, Учитывая условие

нормировки (2.78), в соответствии с (2.77) получаем

п У1 - ж

1 + с^ТЛх)

где

Cu = V2 jwi{x)T(x)dx.

(2.94) (2.94а)

Из (2.94а) находим, например: 1

Ci = V2 lxwi{x)dx==mjy2,

Ся = У2 j(2x-\)wi{x)dx = {2m-\)Y2,

Сг = V2 /(4;сЗ - Ъх) wi {х) dx = (4отз - Зт) /2. -1

Тогда первые члены разложения (2.94) представляются следующим образом:

wi {X) = 1-, [ 1 + 2mi X + 2 (2m, - 1) (2; - 1) +

+ 2 (4m8 ~ 3mi) (4;c ~ 3jc) +...]. (2.95)

2.5.5. Разложение двумерной плотности вероятности. Рассмотрим двумерную плотность вероятности совокупности двух случайных величин. Аналогично (2.77) можно формально представить wii {хи Х2) в виде ряда

оо оо

Ь (1. 2) = Ф1 () Ф2 (х) 2 2 Сиг Qik {Хг) Qar (2) (2.96)

где Qik{xi) и Q2r(x2)-ортогональные нормированные полиномы, соответствующие весовым функциям (pi{xi) и 92(2). Коэффициенты Ckr находим, умножая обе части (2.96) на Qim{xi)Q2n{X2) и дважды интегрируя по Xi я Х2 в области, определяемой весовыми функциями, с использованием условий ортогональности. Тогда в кратной сумме все члены, за исключением одного (fe = m, г=п), обращаются в нуль и в результате

Стп = J S а) Qim (1) Qan (2) i d2 =

-00 -00

= rn,{Q,MQ.na.)). (2.97)

Часто за весовую функцию целесообразно принять одномерные плотности вероятности случайных величин, т. е. ф1 (л:) = ()> ф2() = 2 ( )- Кроме того, во многих практических случаях оказывается, что Сшп = 0 при тфп, и приведенные формулы значительно упрощаются. Вместо разложения в кратный -ряд получаем сумму вида

(i 2) = (i) W 2 Сп Qin (1) Qan (2). (2.98)

где

On- ] ]щ.I. (1, 2)Qin(1) Q2n(2)dxdx,. (2.99)

-00 -00

Так как Qio(a:i) = Q2o(a:2) =о= 1, то из (2.98) видно, что первый член разложения соответствует предположению о независимости случайных величин, а последующие члены определяют поправку, учитывающую вероятностную связь.

Если одномерные распределения случайных величин одинаковы: w {x)=w {х) =w{x)y то разложение (2.98) можно представить в виде

h (%. 2) = (i) (2) 2 Qn М Qn (2.100)

где

(2.101)

Здесь Qn{x)-ортогональные нормированные полиномы относительно весовой функции w{x).

Примером ортогонального разложения является следующее представление двумерной плотности вероятности двух нормиро-ванных гауссовских. случайных величин с коэффициентом корреляции R:

2яУ1-/?а 1

ехр

ехр

---L(x\2Rx,x, + xl)

J л=0

ffn{xi)HM.

(2.102)

где Qn{x)=Hn{x)/Ynl - нормированные полиномом Эрмита и

2.6. ЗАДАЧИ

2.1. Доказать, что начальные моменты распределения Вейбулла

Fg(jc) = l-exp(~x), (la)

ffi,g (а;) = К axf- ехр ( - Я, х'),

а:>0, А,>0, а>0 (li6>

вычисляются по формуле

mkX-f/<T(\+k/a). (2>

Раюсмотреть частные случаи при а=1 (зкопоншадиальное распределение) и при а=2, Х=[{2о^)- (рэлеевское распределение).

2.2. Доказать, что начальные моменты гам,ма-распределения

П^ = Т(ЙГ* ;с>0, Я>0, д>0

вьЕЧ!И1Сляются 1г0 формуле

а 6ета-раапределен(ия

5W- S(a. 6)

(®б)

(4а>

по формуле

Т(а + к)Г{а + Ь) B(a-\-k, b)

mft =

Т(а)Г{а + Ь+к) B{a,b)

2.3. Показать, что для т-раопределвния (распределения Накагамя) г2- I тг\ 1

иачальные моменты

= Г(т) lir) Убедиться, что при /п=1 расоределение (5а) переходит в рэлеевское, а три т=1/2 - в QAHOCTiQpoHiHee нормальное.

2.4. Показать, что для одностороннего нормального распределения

a;g(a:) = У27(яа2) ехр[-;с2/(2а2)], а;>0 (6а)

среднее значение и дисперсия соответственно

т1 = аУ27я, Й2=(1-/я)о2. (66)

Вывести общую формулу для начальных моментов

тн = (2а2)/2 г Г (1/2). (6в)

2.5. Показать, что для распределения Лапласа

uyg(a:) = -exp(- X дг), Я>0 (7а)

имеют место формулы

mgfe-i-O, /n2ft = 2fe=(2)IA2\ >1. (76)

Глава 3

ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН

3.1. распределения вероятностей функций случайных аргументов

3.1.1. Постановка задачи. Решение очень многих практических задач радиотехники, связи и управления сводится к определению по заданной плотности распределения случайных величин плотности распределения другой совокупности случайных величин, получаемой из первой детерминированным функциональным преобразованием.

Рассмотрим исходную совокупность случайных величин Vi={hy hy У In)у для которой известна совместная плотность вероятности wn{xVi). Зададим закон преобразования этой совокупности системой детерминированных функций

УкЧк{х^1)у k=h т. (3.1)