2.2.2. Среднее значение. Простейшая числовая характеристика случайной величины - момент распределения первого порядка- определяет абсциссу центра тяжести плоской фигуры, ограниченной кривой распределения и осью абсцисс и называется математическим ожиданием, или средним значением случайной величины.

Из (2.20) и (2.21) при k=l находим среднее значение непрерывной случайной величины

Щ{1}= Jxwiix)dx (2.22)

-too

п среднее значение дискретной случайной величины

1Ш= 2,yfr = xp. (2.23)

Г

Среднее значение случайной величины характеризует только расположение кривой распределения относительно начала координат. Для центрированной случайной величины g-среднее значение равно нулю, а геометрическая форма кривой плотности та же, что и для случайной величины Размерность среднего значения совпадает с размерностью значений случайной величины.

2.2.3. Центральные моменты. В отличие от моментов которые называют начальными, моменты распределения центрированной случайной величины называют центральными и обозначают \Xk{l}- Для непрерывной случайной величины

](x--m,{l})wi{x)dx, k>2, (2.24)

а для дискретной

HiXr-mADfPr, k>2. (2.25)

Г

Если среднее значение случайной величины равно нулю, то центральные моменты распределения совпадают с начальными. Очевидно, центральный момент первого порядка всегда равен нулю.

2.2.4. Дисперсия. Центральный момент второго порядка называется дисперсией случайной величины и определяется в соответствии с (2.24) и (2.25) по формулам:

для непрерывной случайной величины

\Л1)= ]{x-mfwi{x)dx, (2.26)

для дискретной

И2Ш= E(r-mi)Vr. (2.27)

Отметим, что часто используют обозначение Ме, для среднего значения и D\ для дисперсии случайной величины.

Величину )/называют среднеквадратическим значением случайной величины I. Размерность дисперсии совпадает с размерностью квадрата значений случайной величины, а размерность среднеквадратического значения-с размерностью случайной величины.

Центральный и начальный моменты второго порядка связаны соотношением, которое непосредственно следует из (2.26) или (2.27):

12=2-mi. (2.28)

Обозначим mi{}=a и рассмотрим вероятность Р{\1-а\>г}= \ w.{x)dx, 8>0.

\х-а\г

Так как {х-а)/г'1, то

P(g-a>8}<4- i {x-a)w{x)dx-\ ]{x-a)w{x)dx, т. е.

Р{\1-а\>г}1Х2{1}/г\ (2.29)

Соотношение (2.29) называется неравенством Чебышева. При e,=kV 1X2 из него следует

Pg~a>/й<l/fe (2.29а)

т. е. отклонения g от его среднего, значительно превышающие среднеквадратическое, маловероятны. Таким образом, дисперсия случайной величины характеризует разброс ее значений относительно среднего.

2.2.5. Коэффициенты асимметрии и эксцесса. Среднее и дисперсия не отражают всех особенностей кривой распределения. Одной из них являются симметрия или асимметрия кривой плотности относительно оси, проходящей через центр тяжести. При любом симметричном распределении центральный момент произвольного нечетного порядка равен нулю, что непосредственно видно из (2.24). Поэтому простейший из нечетных моментов - центральный момент третьего порядка:

[гзШ= ]ixm,rwi(x)dx (2.30)

в первом приближении служит характеристикой асимметрии распределения. Его можно выразить через начальные моменты первых трех порядков:

1з=тз-3mim2+2m. (2.31)

Асимметрию распределения принято характеризовать безразмерным отношением

klislV. (2.32)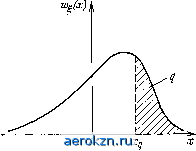

которое называется коэффициентом асимметрии.

В качестве характеристики сглаженности кривой распределения около ее моды используют безразмерный коэффициент эксцесса

7=[i4/2-3.

(2.32а)

Рис. 2.3. Процентная точка

2.2.6. Квантили и процентные точки распределения. Распределение вероятностей случайной величины часто характеризуют квантилями порядка р, т. е. таким значением a:=x*p, которое удовлетворяет уравнению

h{x;)p. (2.33)

Квантиль л:*о,5, которая делит площадь под кривой плотности вероятности на две равные части, называют медианой распределения.

Процентные точки распределения определяются из уравнения (рис. 2.3)

P{l>x,]=\F{Xq) = q (2.34а)

или

XqFl{\-q\ (2.346)

где /~(1-q) - функция, обратная функции распределения. Ясно, что q - процентная точка распределения - совпадает с кван-тилью порядка 1-.

2.3. совокупность случайных величин

2.3.1. Многомерное распределение вероятностей совокупности случайных величин. Некоторые положения теории случайной величины, изложенные ранее, можно обобщить на произвольную конечную совокупность случайных величин i,..., gn. Эту совокупность можно рассматривать как случайную точку в гг-мерном эвклидовом пространстве со случайными декартовыми координатами i=l, п, или как случайный вектор

1=1=аь..., 1пУ (2.35)

в дальнейшем для векторных величин \, х используем обозначения 1, тогда, когда следует указать размерность вектора.

Таким образом, множеством возможных значений совокупности случайных величин является многомерное эвклидово пространство (или область, принадлежащая этому пространству). Необходимо также определить на указанном множестве распределение вероятностей совокупности случайных величин.

По аналогии с функций распределения скалярной случайной величины введем многомерную функцию совместного распределения совокупности случайных величин (векторной случайной величины) [см. (2.35)]

Рь..лЛг^ Хп) = \}]{1г<хЛ (2.36а) lt=i J

или к векторной форме

/ g (xy) = P( <x?}. (2.366)

Многомерная функция совместного распределения векторной случайной величины обладает свойствами, аналогичными свойствам функции распределения скалярной случайной величины. Значения многомерной функции распределения неотрицательны и не превосходят единицы. Если хотя бы один из аргументов Хг=-оо, то значение функции распределения равно нулю, а если все аргументы Хг = оо г=1, п, то значение этой функции равно единице. Кроме того, многомерная функция распределения неубывающая в любом направлении, изменяющемся от -оо к оо.

Однако появляется и новое свойство, присущее многомерной функции совместного распределения. Если п-т аргументов функции (2.36а) обращаются в бесконечность, то эта функция становится функцией совместного распределения остальных т случайных величин. Например,

m, оо,..., oo)-F,...I(a:i,..., Xra) (2.37а)

или в векторной форме

f (х-, оо)=/(х-), (2.376)

Обратное, вообще говоря, неверно, т. е. по распределениям частей совокупности случайных величин нельзя найти совместное распределение всей совокупности. Исключение из этого общего правила составляет совокупность совместно независимых случайных величин, для которой по определению

п)=П^1,(). (2.38)

Пусть \ и т| -два случайных вектора. Для их независимости необходимо и достаточно, чтобы функция их совместного распределения была равна произведению функций распределений каждого из них:

у) = /(х)/я(У)- (2.38а)

2.3.2. Многомерная плотность вероятности. Смешанная производная п-го порядка от гг-мерной функции совместного распределения

......=--t[j;r.- ( >

базывается n-мерной плотностью вероятности совокупности случайных величин gi,..., gn. В векторной форме (2.39а) можно переписать в виде

-±-. (2.396)

Многомерная плотность вероятности векторной случайной величины обладает свойствами, аналогичными свойствам плотности скалярной случайной величины:

W {х^) > О, wn {х^) dx = 1, (2.40)

1 X

где Х^ -п-мерное эвклидово пространство.

Многомерная функция совместного распределения выражается через многомерную плотность при помощи интеграла

F.n{x-) = I wn {п-)йпп, (2.41)

где - область п-мерного эвклидова пространства, определяемая системой неравенств -ooUiXi, г=1, п.

Дифференцируя обе части (2.37а) по переменным Xi,..., Хщ, получаем

4.-.tr {Xi,-, xj= J... wi,..,i{xi..., x )dxm+i ...dXn. (2.42)

- oo -OO

Таким образом, по известной гг-мерной плотности вероятности всегда можно определить плотность вероятности любой группы т случайных величин (lmn) путем интегрирования в бесконечных пределах по остальным п-т переменным.

Обратное, вообще говоря, неверно, т. е. по многомерным плотностям частей совокупности случайных величин нельзя найти плотность вероятностей всей совокупности. Исключение из этого общего правила составляет совокупность совместно независимых случайных величин, для которой (см. (2.38))

.. ..,(1--- п)-11Щ^(д- (2.43)

2.3.3. Числовые характеристики совокупности случайных величин. Наиболее общей числовой характеристикой совокупности п случайных величин является следующий смешанный момент совместного распределения:

оо СХ>

ft..-.ft {ii.-. in}= J... 4-* i..-.i (i. Xn)dxi...dxn,

- oo -CO

(2.44)

где fej -любые положительные числа (включая и нуль), /=1,д. 28

При ki=l, kj=Oy /=1,..., г-1, r+1,..., п из (2.44) получаем среднее значение случайной величины

- оо - оо

= ]xiWii(Xi)dXi=ai.. (2.45)

Смешанный центральный момент второго порядка случайных величин и

Kij = cov{li,lj)= j... J(Xi-a.)x

-оо -,00

= ] ]{Xi-ai){xj-ai.)wi.ij{Xi, Xj)dXidXj (2.46)

- oo -oo

называется ковариацией случайных величин и gj. При г=/ ко-вариация представляет дисперсию случайной величины g-Безразмерное отношение

l,i;=cov(g У/о^.о^ (2.47)

где i = Yvu, называется коэффициентом корреляции случайных величин и gj.

Можно доказать (используя неравенство Буняковского - Шварца), что

Если случайные величины и независимы, то /?.у=0. Обратное утверждение о независимости и при =0 в общем случае несправедливо. Две случайные величины, для которых коэффициент корреляции равен нулю, называются некоррелированными. Таким образом, независимые случайные величины всегда некоррелированы, но не наоборот.

Если ограничиться моментами порядка не выше второго, то совокупность случайных величин ..., можно характеризовать вектором средних

а|=К,..., (2.49)

и ковариационной (корреляционной) матрицей [см. (2.46)]

\l = {Kii) = oG, (2.50)

где R-матрица коэффициентов корреляции, а - диагональная матрица с элементами а^. , =1, п, на главной диагонали.

Ковариационная матрица К| представляет симметричную, положительно определенную матрицу размером пХп. Положитель-

ная определенность матрицы К| означает, что для любых действительных чисел Яь ..., Кп

f=i /=1

(2.51а) (2.516)

или в векторной форме ГК?>0,

где вектор-строкаЧ^= (Хь..., Кп). Необходимое и достаточное условие положительной определенности матрицы К| записывается в виде

det К|>0.

(2.51в)

2.3.4. Условные функции распределения. Рассмотрим совокупность gi,... , In зависимых случайных величин и используем правило умножения для определения вероятности пересечения событий 11 х^1 и lm4-ig,n , где g -малая окрестность

точки Х^т+ь

откуда [см. (2.41)]

I 1 V

Р 11 <Сх I е I = --- -

ym X

Когда область g стягивается в точку xV+i, получаем функцию

т-\-\

jn m+1 m+1

I a. (x?)dx-

(2.52)

которая называется условной функцией распределения случайного вектора при условии, что зависимый от него случайный

вектор m+l=Xm+l. 30

Для совокупности двух случайных величин (az=2, т=1) получаем из (2.52)

00

(2.53)

Вычисляя смешанную производную от F(xixV+i) по лгь... , хт, получаем условную плотность вероятности

W (х^

(2.54)

Для совокупности двух случайных величин из (2.54) следует

w{Xi\x)= -.

(2.55)

Формулу (2.54) можно переписать в форме, аналогичной форме правила умножения для случайных событий:

ауЛх ) = ш^ (х^+,)ау(х-х^,)ш^. (х-) ш (х;;, х-). (2.56)

1 m-f-l . 1

а также

rt-i

\п (ху)=а;, (i) n(+ixf).

(2.57)

Заметим, что этот аналог правила умножения для случайных величин выражается через плотности вероятности, а не через функции распределения.

Из (2.56) следуют аналоги формулы полной вероятности

(2.58)

и формулы Байеса

I V (C+i)-(<x+.X+i-

(2.59)

Для совокупности двух случайных величин из (2.58) из (2.59) получаем

04.(1)= wi{x)w{xAx2)dx, (2.60)

- 00

W {х^\х^) = -. (2.61)

- 00

2.3.5. Условны^ среднее значение и дисперсия. При помощи условных плотностей вероятности можно определить и условные числовые характеристики случайных величин.

Если имеется совокупность зависимых случайных величин gb..., 1пу то условное среднее значение случайной величины gi

при 2 = х 2

НА-п = т^{Ш1хЧ]= \xw[xAx-dx. (2.62)

2 ~ 00

а условная дисперсия

[2= X } = ]jx~а^п у W {х^\х1) dx (2.63)

2.4. нормальное распределение вероятностен

2.4.1. Многомерная нормальная плотность вероятности. Важнейшим для практических приложений является нормальное распределение совокупности случайных величин, которое определяется следующим выражением многомерной плотности вероятности этой совокупности:

(X) = Р { - 4- (2.64)

где К~ - матрица, обратная матрице Kg.

Из (2.64) следует, что нормальное распределение совокупности случайных величин полностью определяется вектором средних значений а^ и ковариационной матрицей К|.

Совокупность случайных величин, подчиняющуюся нормальному закону распределения, называют гауссовской.

Матричному представлению (2.64) многомерной нормальной плотности вероятности соответствует следующее ее выражение через скалярные величины:

п п

2D {ik=i

(2.65)

где ai=mi{li}, oi = ii2{U}. D=cletR, R= J - матрица коэффициентов корреляции размером пХп, а Dik - алгебраическое дополнение элемента R.if в определителе D. Таким образом п-мерная нормальная плотность вероятности зависит от 2л параметров (а^, Gi) и от п(п-\)12 параметров Ri. i.

Можно доказать, что любая часть гауссовской совокупности случайных величин также является гауссовской. Обратное утверждение, вообще говоря, неверно (см. пример в [1, с. 51]).

2.4.2. Гауссовская случайная величина. Из (2.65) при п-\ находим нормальную плотность вероятности одной гауссовской случайной величины

которая определяется двумя параметрами: средним значением и дисперсией а^.

Как видно из рис. 2.4, кривые плотности нормального распределения при различных значениях дисперсии унимодальны, т. е. имеют один максимум в точке х=а. Кривая плотности в полосе fl±3a ограничивает 99,7% общей площади, т. е. с вероятностью 0,997 значения гауссовской случайной величины попадают в интервал (а-30, а+Ъа).

Нетрудно показать, что точки перегиба, в которых кривая плотности имеет максимальную крутизну, определяются из равенства х=а±о. При о-оо кривая распределения сливается с осью абс-цисс, а при она переходит в дельта-функцию:

lim-i=-exp{~- Функция распределения гауссовской случайной величины

Интеграл

называемый интегралом Лапласа, представляет функцию распределения нормированной стандартной гауссовской случайной величины при а=0, а=1. Имеются многочисленные таблицы интегра-йа Лапласа, т. е. функции стандартного нормального распределения (см., например, [2]). Эти таблицы можно использовать для 2-87 35